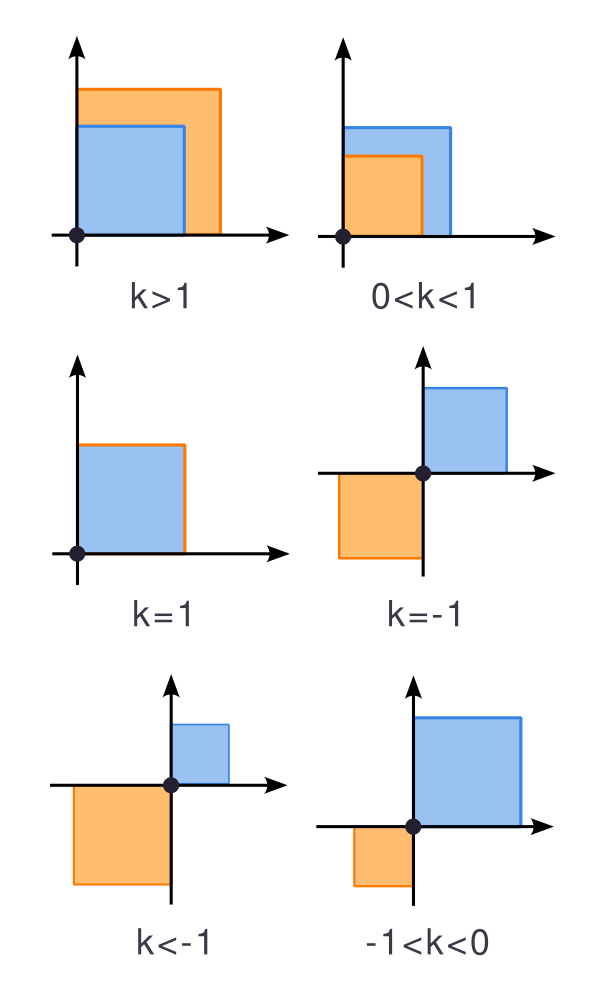
Равномерное масштабирование

Матрица изотропного масштабирования

Это диагональная скалярная матрица c заданным ненулевым коэффициентом масштабирования
$$\mathbf{S}=\begin{pmatrix}k&0&0\\0&k&0\\0&0&k\end{pmatrix}$$
Свойства:
Является преобразованием гомотетии с неподвижной точкой в начале координат
Ядро и образ $\mathbf{S}:V\to W$ определяются, как:
$$\ker(\mathbf{S})=\{\mathbf{0}\},\ \mathrm{im}(\mathbf{S})=W$$
Определитель матрицы равен произведению её диагональных элементов (коэффициентов)
Обратная матрица — диагональная скалярная матрица с обратным коэффициентом
$$\mathbf{S}^{-1}=\begin{pmatrix}\frac{1}{k}&0&0\\0&\frac{1}{k}&0\\0&0&\frac{1}{k}\end{pmatrix}$$