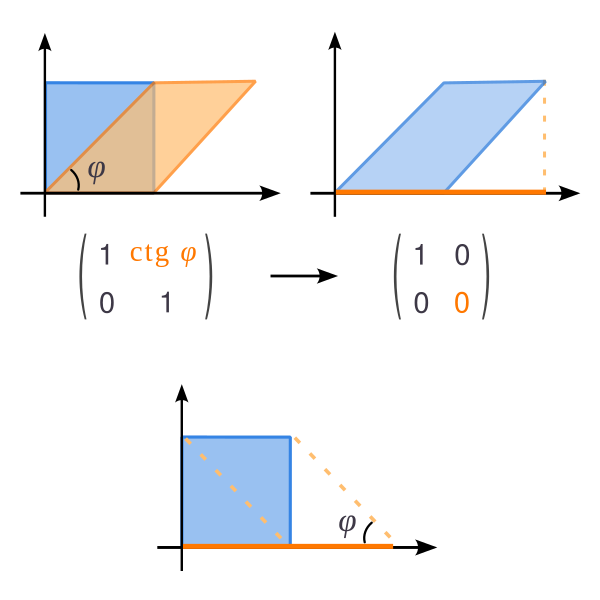
Матрица косоугольной проекции
Неортогональная проекция
- Это последовательная композиция матрицы сдвига и матрицы ортогональной проекции
- $$\begin{pmatrix}1&0\\0&0\end{pmatrix}\begin{pmatrix}1&2\\0&1\end{pmatrix}=\begin{pmatrix}1&2\\0&0\end{pmatrix}$$
- Свойства:
- Является идемпотентным преобразованием, не является подобием, снижает размерность
- $$(\mathbf{S}\circ\mathbf{H})^2=\mathbf{S}\circ\mathbf{H}$$
- Ядро и образ $\mathbf{S}_{xy}\circ\mathbf{H}$, где сдвиг $\mathbf{H}:V\to W$ и проекция $\mathbf{S}_{xy}:W\to W^{'}$, определяются, как:
- $$\ker(\mathbf{S}_{xy}\circ\mathbf{H})=\{\mathbf{w}\ |\ \mathbf{w}\perp xy\}$$
- $$\mathrm{im}(\mathbf{S}_{xy}\circ\mathbf{H})=\{\mathbf{w^{'}}\ |\ \mathbf{w^{'}}\in xy\}$$
- Определитель матрицы всегда равен нулю
- Обратной матрицы не существует