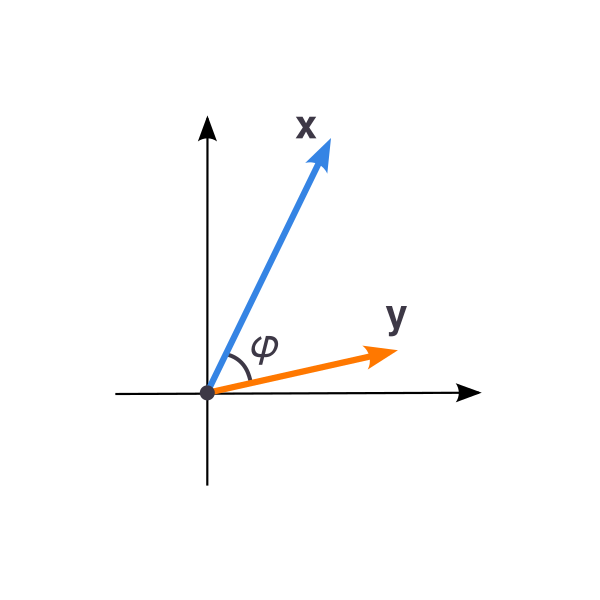
Угол между векторами
Косинусное сходство между векторами
- Угол между векторами определяется через их скалярное произведение и произведение длин
- $$\cos\varphi=\frac{\mathbf{x}\cdot\mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|}\Rightarrow\varphi=\arccos\frac{\mathbf{x}\cdot\mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|}$$
- Если $\varphi\in(0^{\circ};90^{\circ})$, то $\cos\varphi\geqslant 0,\ \mathbf{x}\cdot\mathbf{y}\geqslant 0$
- Если $\varphi\in(90^{\circ};180^{\circ})$, то $\cos\varphi\leqslant 0,\ \mathbf{x}\cdot\mathbf{y}\leqslant 0$
- Если $\varphi=90^{\circ}$, то $\cos\varphi=0,\ \mathbf{x}\cdot\mathbf{y}=0$
- Если $\varphi=0^{\circ}$, то $\cos\varphi=1,\ \mathbf{x}\cdot\mathbf{y}=\|\mathbf{x}\|\|\mathbf{y}\|$
- Косинус угла между единичными векторами равен их скалярному произведению: $\cos\varphi=\hat{\mathbf{x}}\cdot\hat{\mathbf{y}}$