Как рассчитать определитель матрицы?

Значение определителя матрицы

Для матрицы первого порядка определитель равен значению её единственного элемента
$$\begin{vmatrix}a_{11}\end{vmatrix}=a_{11}$$
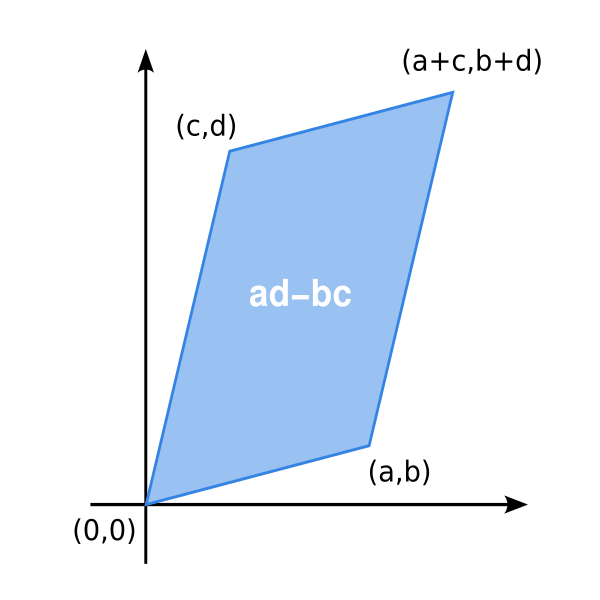
Для матрицы второго порядка (размера $2\times 2$):
$$\begin{vmatrix}a&c\\b&d\end{vmatrix}=ad-bc$$
Для матрицы третьего порядка (размера $3\times 3$):
$$\small a_{11}\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}-a_{12}\begin{vmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{vmatrix}+a_{13}\begin{vmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{vmatrix}$$
В общем случае — это сумма произведений элементов матрицы по всем перестановкам чисел $1,2,\ldots,n$ с учетом их чётности
$$\small\sum_{\alpha_1,\alpha_2,\ldots,\alpha_n}(-1)^{N(\alpha_1,\alpha_2,\ldots,\alpha_n)}\cdot a_{1\alpha_1}a_{2\alpha_2}\dots a_{n\alpha_n}$$