Определитель матрицы
Детерминант матрицы
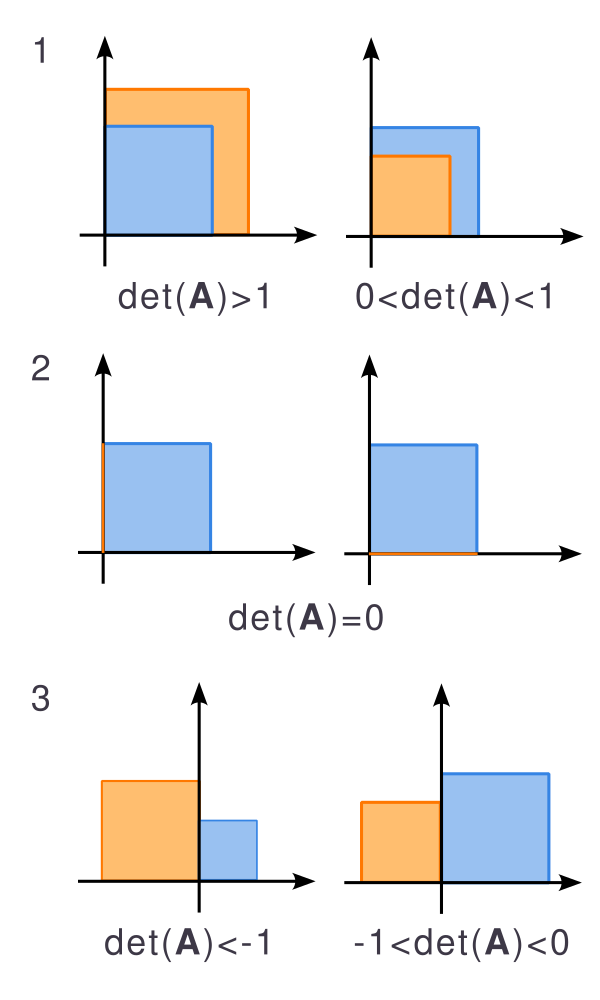
- Это число (мера), характеризующее «растяжение» или «сжатие» многомерного пространства после преобразования квадратной матрицей
- $$\det(\mathbf{A})\quad |\mathbf{A}|\quad\Delta(\mathbf{A})$$
- Больше 0 — сохранение ориентации с «растяжением» или «сжатием» пространства
- Равен 0 — снижение размерности, ранг матрицы преобразования неполный
- Меньше 0 — изменение ориентации с «растяжением» или «сжатием» пространства
- Абсолютное значение определителя матрицы размера $2\times 2$ — это площадь параллелограмма, образованного её векторами (столбцами)