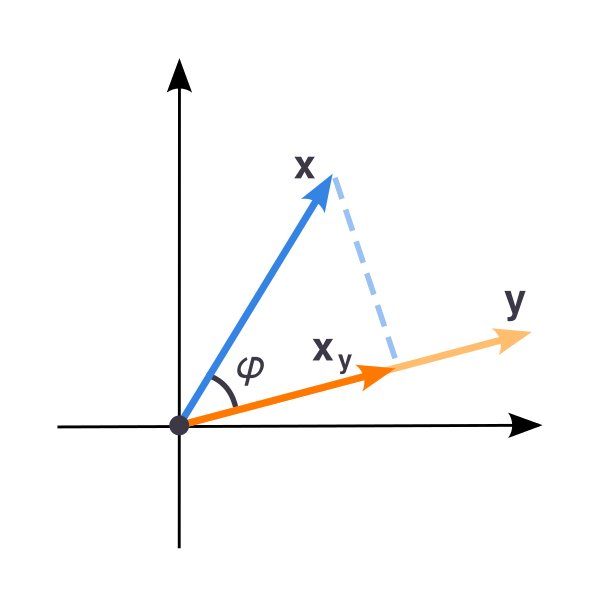
Проекция вектора на вектор
Скалярная и векторная проекция
- Скалярная проекция (длина проекции) одного вектора на другой равна произведению длины первого на косинус угла между векторами
- $$\|\mathbf{x}_{\mathbf{y}}\|=\|\mathbf{x}\|\cos\angle(\mathbf{x},\mathbf{y})$$
- Скалярное произведение может быть выражено, как произведение длины проекции первого вектора на второй и длины второго вектора
- $$\mathbf{x}\cdot\mathbf{y}=\|\mathbf{x}_{\mathbf{y}}\|\|\mathbf{y}\|$$
- Векторная проекция показывает длину одного вектора в направлении другого вектора
- $$\mathbf{x}_{\mathbf{y}}=\|\mathbf{x}_{\mathbf{y}}\|\hat{\mathbf{y}}$$
- Если векторы ортогональны, то их скалярное произведение и взаимные проекции равны нулю