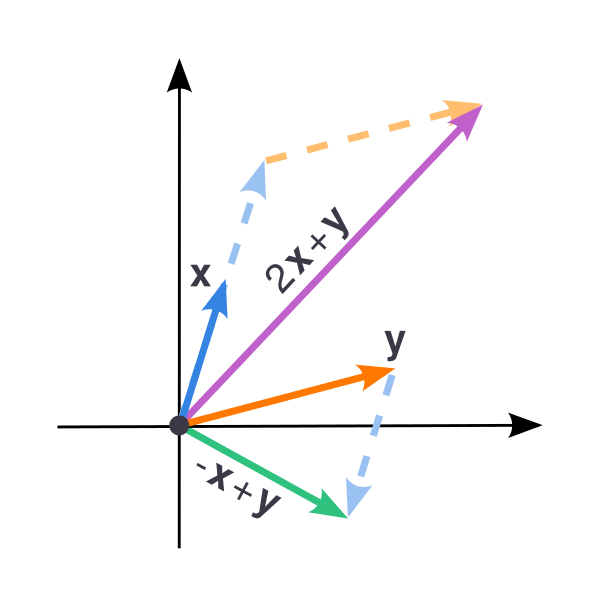
Линейная комбинация векторов
Выражение вектора через другие векторы
- Для векторов $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_k\in\mathbb{R}^n$ — это операция вида $\lambda_1\mathbf{x}_1+\lambda_2\mathbf{x}_2+\cdots+\lambda_k\mathbf{x}_k$, где $\lambda_1,\lambda_2,\ldots,\lambda_k$ являются коэффициентами линейной комбинации
- $$\sum_{i=1}^{k}\lambda_i\mathbf{x}_i$$
- Любой вектор может быть выражен линейной комбинацией векторов различными способами
- $$\mathbf{z}=\lambda\mathbf{x}+\gamma\mathbf{y}=\alpha\mathbf{v}+\beta\mathbf{u}$$
- Число векторов в линейной комбинации обычно конечно, включая ноль и единицу