Теорема Лагранжа
Формула конечных приращений
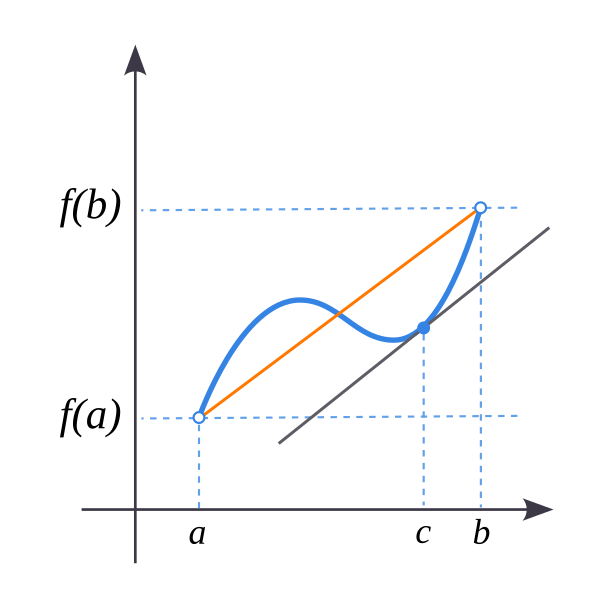
- Если функция $f(x)$ непрерывна на отрезке $[a,b]$ и дифференцируема на интервале $(a,b)$, то на интервале $(a,b)$ найдётся такая точка $c$, что:
- $$f'(c)=\frac{f(b)-f(a)}{b-a}$$
- Геометрический смысл: на данном отрезке кривой существует касательная, параллельная хорде, проходящей через точки $a$ и $b$
- Физический смысл: производная функции в точке $c$ — это средняя скорость движения тела на данном промежутке