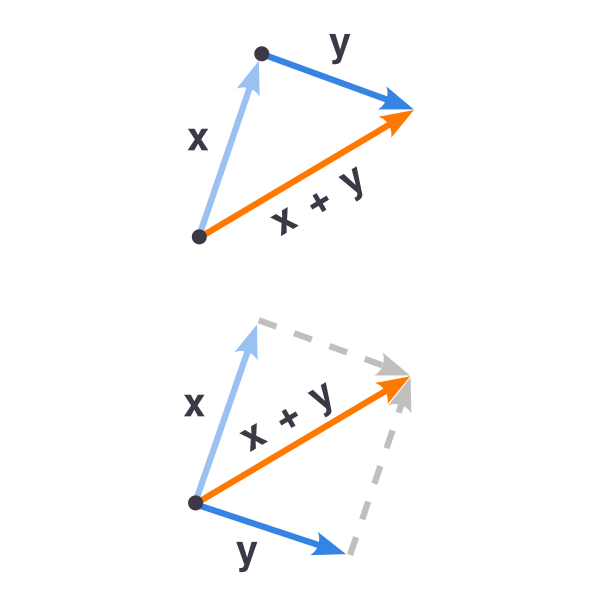
Сложение векторов

Покомпонентное сложение

Результатом сложения векторов является новый вектор из сумм их соответствующих компонент
$$\mathbf{x}+\mathbf{y}=(x_1+y_1,x_2+y_2,\ldots,x_n+y_n)$$
Это композиция параллельных переносов
$$\mathrm{T}_{\vec{x}+\vec{y}}=\mathrm{T}_{\vec{y}}\circ\mathrm{T}_{\vec{x}}$$
Свойства:
Коммутативность: $\mathbf{x}+\mathbf{y}=\mathbf{y}+\mathbf{x}$
Ассоциативность: $(\mathbf{x}+\mathbf{y})+\mathbf{z}=\mathbf{x}+(\mathbf{y}+\mathbf{z})$
Существование нейтрального элемента
$$\exists\mathbf{0}\in V:\mathbf{x}+\mathbf{0}=\mathbf{0}+\mathbf{x}=\mathbf{x}$$
Существование обратного элемента
$$\exists(-\mathbf{x})\in V:\mathbf{x}+(-\mathbf{x})=\mathbf{0}$$