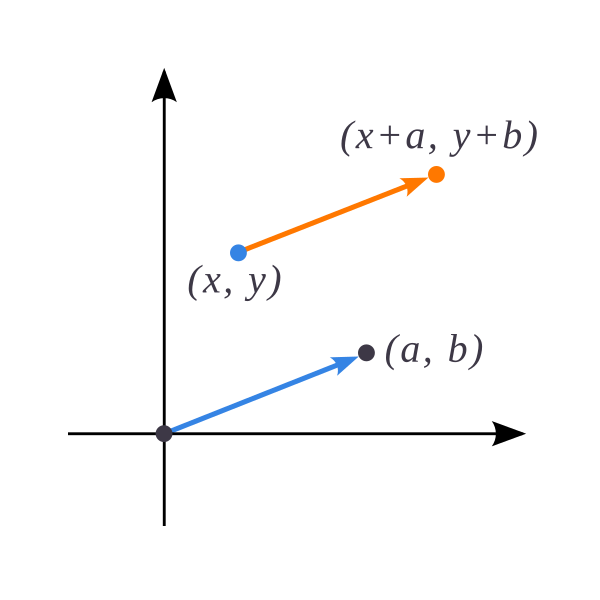Параллельный перенос плоскости
Трансляция, сдвиг всех точек плоскости
- Это движение плоскости, при котором все её точки перемещаются в одном и том же направлении на одно и то же расстояние
- $$\mathrm{T}_{(a,b)}(x,y)=(x+a, y+b),\quad \vec{v}=(a,b)$$
- При параллельном переносе плоскости не остается ни одной неподвижной точки
- Параллельный перенос плоскости сохраняет ориентацию (направление)
- $$\forall\vec{a}\quad f(\vec{a})=\vec{a}$$
- Параллельный перенос на нулевой вектор является тождественным преобразованием
- $$\mathrm{T}_{\vec{0}}(X)=\mathrm{Id}(X)=X$$
- Плоскость бесконечна и может быть сдвинута в любом направлении на любой вектор