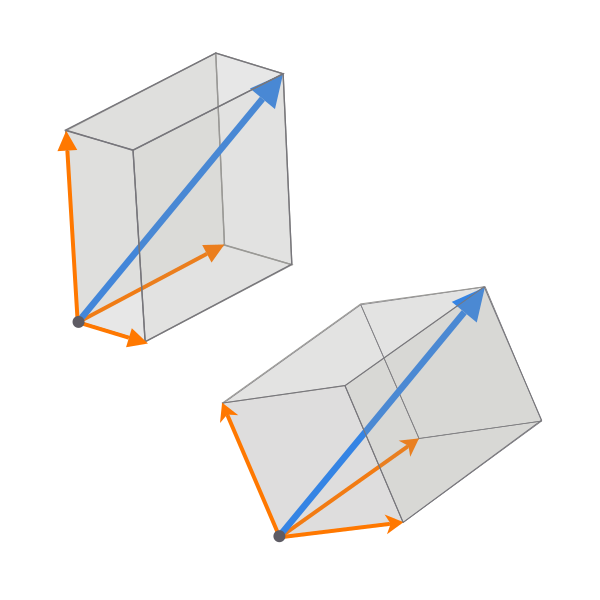
Базис пространства
От др. греч. — «основа»
- Это последовательность линейно независимых векторов пространства: $B=(\mathbf{e}_1,\mathbf{e}_2,\ldots,\mathbf{e}_n)$
- Любой вектор может быть разложен по базису единственным образом, причём коэффициенты такой линейной комбинации называются его координатами относительно данного базиса
- $$\mathbf{x}=\lambda_1\mathbf{e}_1+\lambda_2\mathbf{e}_2\Rightarrow\mathbf{x}=\begin{bmatrix}\lambda_1\\ \lambda_2\end{bmatrix}$$
- Ортогональный базис — базис из векторов, угол между которыми равен $90^\circ$
- Ортонормированный базис — ортогональный базис из единичных векторов
- Базис вместе с точкой начала координат задают аффинную систему координат пространства