Линейная оболочка
Множество всех линейных комбинаций векторов
- Это множество всех линейных комбинаций некоторого конечного множества векторов
- $$(V,F,+,\cdot)\quad S=\{\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_k\},\ S\subset V$$
- $$\small\mathrm{span}(S)=\left\{{\left.\sum_{i=1}^{k}\lambda_{i}\mathbf{x}_{i}\;\right|\;k\in\mathbb{N},\mathbf{x}_{i}\in S,\lambda_{i}\in F}\right\}$$
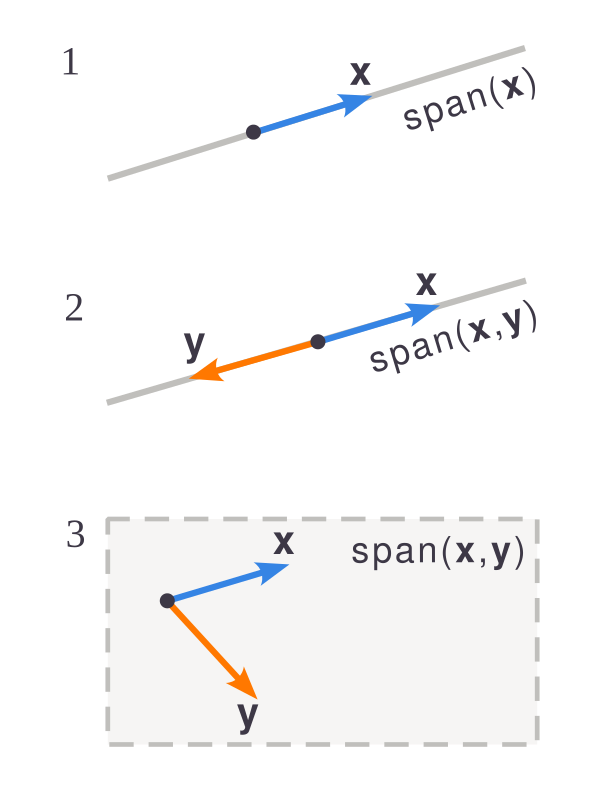
- Для одного вектора — множество всех его скалярных кратных: $\mathbb{R}^1$ (прямая)
- Для 2 коллинеарных векторов — множество всех коллинеарных им векторов: $\mathbb{R}^1$ (прямая)
- Для 2 неколлинеарных векторов — множество всех векторов образованной ими плоскости: $\mathbb{R}^2$