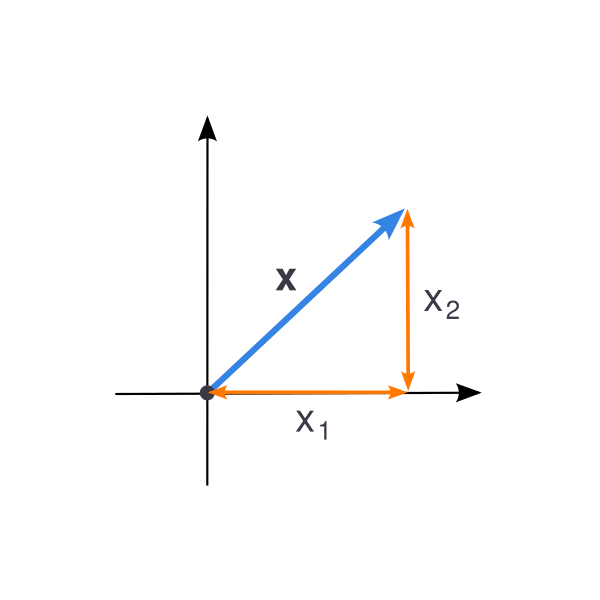Длина вектора
Результат векторной нормы
- Это число, результат применения функции длины (нормы) к вектору в нормированном пространстве
- $$\|\mathbf{x}\|_{p}=\left(\sum_{i}|x_{i}|^{p}\right)^{1/p}$$
- Длина вектора может быть определена по-разному, в зависимости от заданной в нормированном пространстве нормы: $\|\mathbf{x}\|_1,\|\mathbf{x}\|_2,\|\mathbf{x}\|_{\infty}$
- Например: на плоскости с евклидовой нормой длина двумерного вектора равна длине гипотенузы прямоугольного треугольника, образованного координатами вектора и самим вектором
- $$\|\mathbf{x}\|_2=\sqrt{x_{1}^{2}+x_{2}^{2}}$$