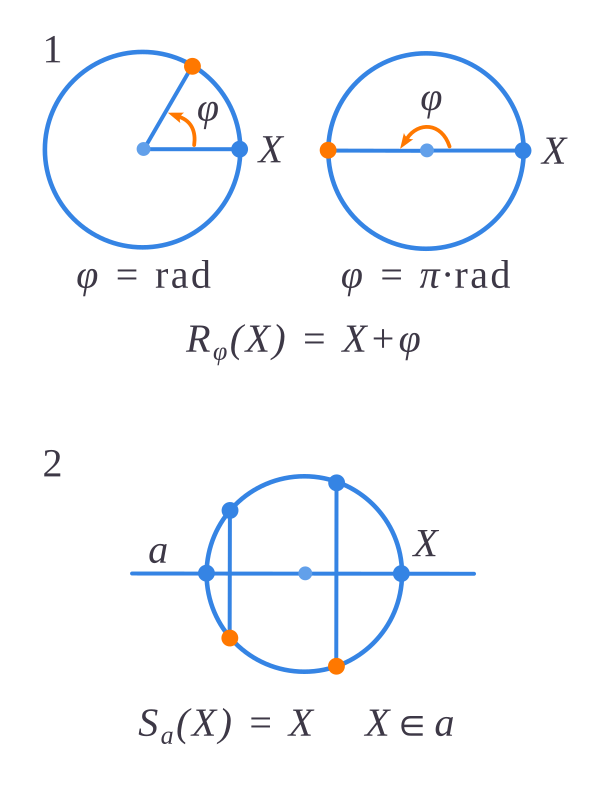Классификация движений окружности
По числу неподвижных точек
- Нет неподвижных точек — это поворот всех точек окружности против часовой стрелки на ненулевой угол (в радианах или градусах)
- $$\mathrm{R}_{\varphi}(X)=X+\varphi$$
- $$\varphi\in[0^{\circ};360^{\circ})\quad\varphi\in[0\ \mathrm{rad};2\pi\ \mathrm{rad})$$
- Две неподвижные точки — это отражение всех точек окружности относительно прямой, проходящей через центр окружности и две противоположные точки
- $$\mathrm{S}_{a}(X)=X\Rightarrow X\in a$$
- Более двух неподвижных точек — это $\mathrm{Id}$ или тождественное преобразование, поворот всех точек окружности на нулевой угол
- $$\mathrm{Id}(X)=\mathrm{R}_{0^{\circ}}(X)=X$$
- Окружность — это фигура из всех точек плоскости, находящихся на одинаковом расстоянии от некоторой фиксированной точки