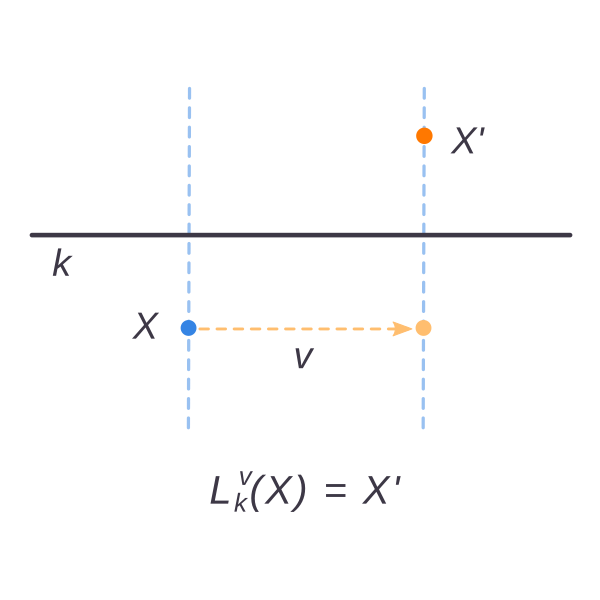Скользящая симметрия плоскости

Композиция трёх отражений

Это движение плоскости — композиция параллельного переноса вдоль некоторой прямой и отражения относительно этой же прямой
$$\mathrm{L}_{k}^{\vec{v}}=\mathrm{S}_{k}\circ\mathrm{T}_{\vec{v}}$$
При скользящей симметрии плоскости не остается ни одной неподвижной точки
Скользящая симметрия меняет ориентацию
Обладает свойством коммутативности
$$\mathrm{S}_{k}\circ\mathrm{T}_{\vec{v}}=\mathrm{T}_{\vec{v}}\circ\mathrm{S}_{k}$$
Скользящая симметрия является композицией трех осевых симметрий вдоль прямых, которые не параллельны и не пересекаются в одной точке