Смена базиса
Переход к другому базису
- Один и тот же вектор, выраженный в разных базисах, имеет разные координаты
- $$\mathbf{v}=\alpha\mathbf{x}+\beta\mathbf{y}\quad\mathbf{v}=\alpha^\prime\mathbf{x}^\prime+\beta^\prime\mathbf{y}^\prime$$
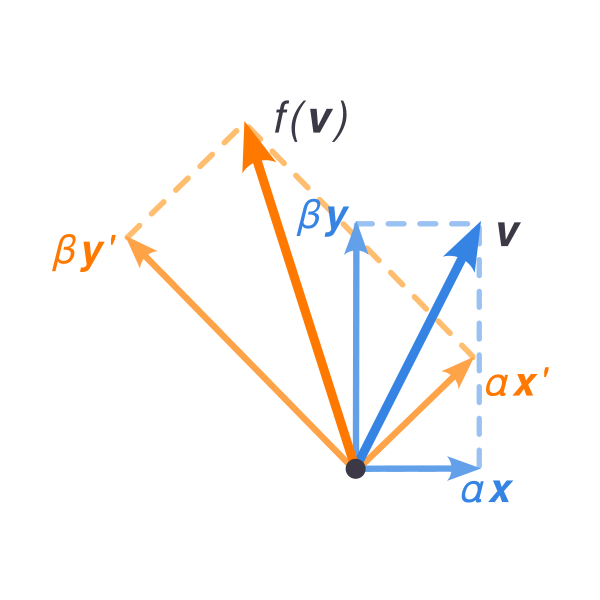
- Смена базиса с сохранением координат каждого вектора является линейным преобразованием пространства, меняющим все его векторы
- $$\mathbf{v}=\alpha\mathbf{x}+\beta\mathbf{y}\quad f(\mathbf{v})=\alpha\mathbf{x}^\prime+\beta\mathbf{y}^\prime$$
- При выражении векторов нового базиса через векторы исходного базиса коэффициенты этих линейных комбинаций однозначно определяют любое линейное преобразование пространства
- $$\mathbf{x}^\prime=\lambda_1\mathbf{x}+\lambda_2\mathbf{y}\Rightarrow\mathbf{x}^\prime=\begin{bmatrix}\lambda_1\\ \lambda_2\end{bmatrix}$$
- $$\mathbf{y}^\prime=\lambda_3\mathbf{x}+\lambda_4\mathbf{y}\Rightarrow\mathbf{y}^\prime=\begin{bmatrix}\lambda_3\\ \lambda_4\end{bmatrix}$$