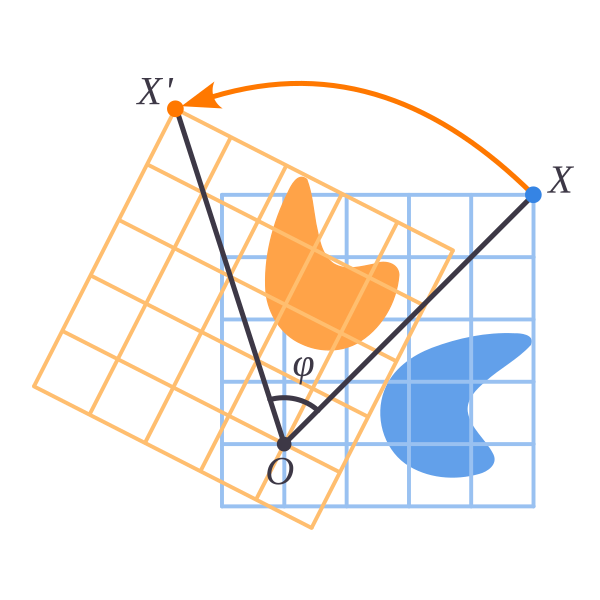
Поворот плоскости
Вращение, осевая симметрия
- Это движение плоскости относительно центра вращения в положительном направлении на некоторый угол (против часовой стрелки)
- $$\mathrm{R}_{\varphi}^{(0,0)}(x,y)=(x',y')$$
- $$x'=x\cos\varphi-y\sin\varphi$$
- $$y'=x\sin\varphi+y\cos\varphi$$
- При повороте плоскости существует только одна неподвижная точка (центр вращения)
- Собственное вращение плоскости сохраняет ориентацию (направление)
- Оборот — это поворот на полный угол $(360^\circ)$
- Поворот плоскости на нулевой угол является тождественным преобразованием
- $$\mathrm{R}_{0^\circ}(X)=\mathrm{Id}(X)=X$$
- Плоскость можно представить как бесконечное множество концентрических окружностей