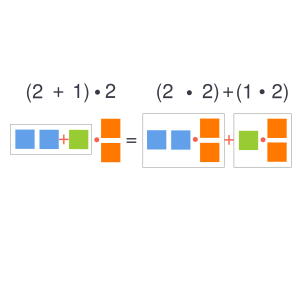
Дистрибутивность операции умножения относительно сложения и вычитания

Правило раскрытия скобок

От лат. distributivus — «распределительный»
Если все слагаемые содержат общий множитель, то его можно вынести за скобки, и наоборот
$$x \cdot (a + b) = (x \cdot a) + (x \cdot b)$$
$$(a + b) \cdot x = (a \cdot x) + (b \cdot x)$$
Если уменьшаемое и вычитаемое содержат общий множитель, то его можно вынести за скобки
$$x \cdot (a - b) = (x \cdot a) - (x \cdot b)$$
$$(a - b) \cdot x = (a \cdot x) - (b \cdot x)$$